Pytorch 04. Softmax Regression

이 포스트는 Github 접속 제약이 있을 경우를 위한 것이며, 아래와 동일 내용을 실행 결과와 함께 Jupyter notebook으로도 보실 수 있습니다.
You can also see the following as Jupyter notebook along with execution result screens if you have no trouble connecting to the Github.

소프트맥스 회귀(Softmax Regression)

다중 (n 개) 클래스 분류 문제에서 ‘독립 변수 X’가 입력되었을 때, 각 클래스에 해당될 확률을 구하는 방법이며, n개 각각 확률의 총합은 1이 되도록 한다.
예로써,k개의 적성검사항목을 통해, n개 종류의 성향별 점수가 나왔고, 이 성향별 점수를 확률적으로 normalize하여, 어느 성향 타입인지 매칭(판별)한다.

Softmax function (소프트맥스 함수)

어떤 값들로 구성된 n개 행렬 원소를 받으면, 이를 normalize 하는 개념으로, 0~1 사이의 값으로 된 n 개의 행렬 원소로 재구성 하여 반환하는데, 원소들의 총합은 1이다.

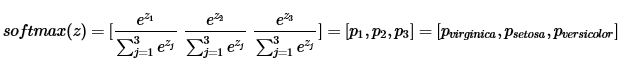
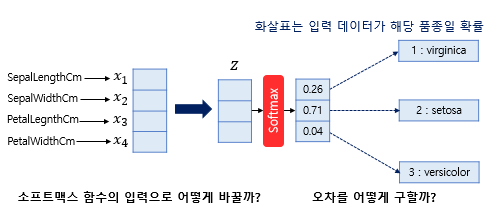
image-center

k차원의 독립변수 x를 ‘k가 아닌 다른 차원’의 class로 분류할때, softmax function으로 입력되는 Z 값은?
Linear regression에서는 k개의 독립변수 x에 대해서, W는 k개, 즉 k x 1 차원이였으나, n개로 분류해야하는 상황에서는 W는 k x n 차원이 되어, n개를 분류하는 가중치 계산을 추가로 진행한다.

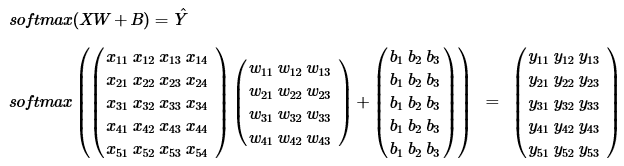
Cost function

소프트맥스 함수의 최종 비용 함수에서 k가 2라고 가정하면 결국 로지스틱 회귀의 비용 함수와 같음.

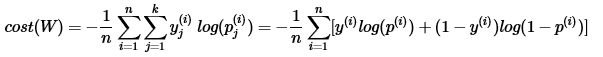
F.cross_entropy(z, y) 함수

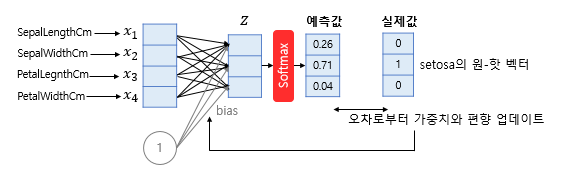
entropy() input인 z는 k차원의 독립 변수 x에 가중치 w,b가 반영된 결과로 n차원임. (z1,z2, … zn) class분류 정답 Y의 one-hot vector와 비교를 위해, z값들을 softmax를 통해 normalize한다. cross entropy로 cost 계산하기 위해, softmax 결과를 log 취하고, one-hot vector (class분류 정답 Y)과 계산한다. 이 일련의 과정은 다음과 같이 요약 표현된다.
1st method (Low level) hypothesis = F.softmax(z, dim=1)
y_one_hot = torch.zeros_like(hypothesis)
y_onehot.scatter(1, y.unsqueeze(1), 1)
cost = (y_one_hot * -torch.log(hypothesis)).sum(dim=1).mean()
위 수식의 log 함수와 softmax함수를 다음과 같이 대체가능
torch.log(hypothesis) = torch.log(F.softmax(z, dim=1)) = F.log_softmax(z, dim=1)
또한, 위 수식에서 y를 one_hot vector로 변환하는 작업을 F.nll_loss() 함수를 써서 생략가능
2nd method (high level)
cost = F.nll_loss(F.log_softmax(z, dim=1), y)
*(nll : Negative Log Likelihood)
3rd method (high level) : F.nll_loss()와 F.log_softmax()를 포함하여,
cost = F.cross_entropy(z, y)
= F.CrossEntropyLoss(z, y)
(*여기서 z의 마지막 차원(특성값, 독립변수 개수)과 y의 최대값(Class 분류를 위한 Label 값보다 1작은 값)은 같아야 함.)

소프트맥스 회귀 구현

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

torch.manual_seed(1)

x_train = [[1, 2, 1, 1],
           [2, 1, 3, 2],
           [3, 1, 3, 4],
           [4, 1, 5, 5],
           [1, 7, 5, 5],
           [1, 2, 5, 6],
           [1, 6, 6, 6],
           [1, 7, 7, 7]]
y_train = [2, 2, 2, 1, 1, 1, 0, 0]
x_train = torch.FloatTensor(x_train)
y_train = torch.LongTensor(y_train)

Low level code

cost 함수 계산을 ‘1st method’으로 진행
y_train은 8x1 vector이나 3개의 class이므로, y의 one hot vector는 8 x 3이어한다. 그리고 W는 4 x 3 vector임.

y_one_hot = torch.zeros(8, 3)
y_one_hot.scatter_(1, y_train.unsqueeze(1), 1)

W = torch.zeros((4, 3), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

optimizer = optim.SGD([W, b], lr=0.1)

nb_epochs = 1000
for epoch in range(nb_epochs + 1):

    hypothesis = F.softmax(x_train.matmul(W) + b, dim=1) 

    cost = (y_one_hot * -torch.log(hypothesis)).sum(dim=1).mean()

    optimizer.zero_grad()
    cost.backward()
    optimizer.step()

    if epoch % 100 == 0:
        print('Epoch {:4d}/{} Cost: {:.6f}'.format(epoch, nb_epochs, cost.item()))

High level code

cost 함수 계산을 ‘3rd method’으로 진행
option으로 nn.Module을 적용한 방법 추가 (# 주석 처리함)

W = torch.zeros((4, 3), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

# option
# 4개의 특성을 가지고 3개의 클래스로 분류. input_dim=4, output_dim=3.
# model = nn.Linear(4, 3)

optimizer = optim.SGD([W, b], lr=0.1)
# optimizer = optim.SGD(model.parameters(), lr=0.1)

nb_epochs = 1000
for epoch in range(nb_epochs + 1):

    z = x_train.matmul(W) + b
    # prediction = model(x_train)
    
    cost = F.cross_entropy(z, y_train)
    # cost = F.cross_entropy(prediction, y_train)

    optimizer.zero_grad()
    cost.backward()
    optimizer.step()

    if epoch % 100 == 0:
        print('Epoch {:4d}/{} Cost: {:.6f}'.format(epoch, nb_epochs, cost.item()))

Advanced level code

nn.Module을 상속받은 클래스로 구현

class SoftmaxClassifierModel(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = nn.Linear(4, 3)

    def forward(self, x):
        return self.linear(x)

model = SoftmaxClassifierModel()

optimizer = optim.SGD(model.parameters(), lr=0.1)

nb_epochs = 1000
for epoch in range(nb_epochs + 1):

    prediction = model(x_train)

    cost = F.cross_entropy(prediction, y_train)

    optimizer.zero_grad()
    cost.backward()
    optimizer.step()

    if epoch % 100 == 0:
        print('Epoch {:4d}/{} Cost: {:.6f}'.format(epoch, nb_epochs, cost.item()))

소프트맥스 회귀(Softmax Regression)

Ethan