이 포스트는 Github 접속 제약이 있을 경우를 위한 것이며, 아래와 동일 내용을 실행 결과와 함께 Jupyter notebook으로도 보실 수 있습니다.
You can also see the following as Jupyter notebook along with execution result screens if you have no trouble connecting to the Github.
Hypothesis and Cost
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
x_data = [1, 2, 3, 4, 5]
y_data = [1, 2, 3, 4, 5]
plt.plot(x_data, y_data, 'o')
plt.ylim(0, 8)
Hypothesis
x_data = [1, 2, 3, 4, 5]
y_data = [1, 2, 3, 4, 5]
W = tf.Variable(2.0)
b = tf.Variable(0.5)
hypothesis = W * x_data + b
- 변수 정의 결과 확인 방법
W.numpy(), b.numpy() hypothesis.numpy() - data 및 변수 초기값을 그래프로 확인하기
plt.plot(x_data, hypothesis.numpy(), 'r-') plt.plot(x_data, y_data, 'o') plt.ylim(0, 8) plt.show()
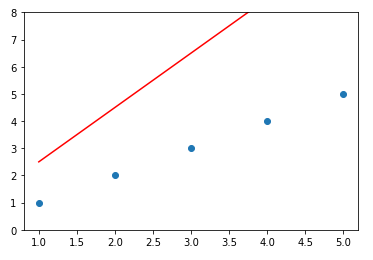
Cost
tf.square & tf.reduce_mean 기능 확인하기
tf.square(3)
v =[1., 2., 3., 4.]
tf.reduce_mean(v)
tf.square(hypothesis - y_data)
GradientTape 기능 확인하기
x = tf.constant(3.0)
with tf.GradientTape() as g:
g.watch(x)
y = x * x # x^2
dy_dx = g.gradient(y, x) # Will compute to 6.0
print(dy_dx)
with tf.GradientTape() as tape:
hypothesis = W * x_data + b
cost = tf.reduce_mean(tf.square(hypothesis - y_data))
W_grad, b_grad = tape.gradient(cost, [W, b]) # Cost 함수의 변수 W, b에 대해 gradient를 구함.
W_grad.numpy(), b_grad.numpy()
Update Parameters
learning_rate = 0.01
W.assign_sub(learning_rate * W_grad) # W 값에서 learning_rate * W_grad를 뺀 값을 다시 W에 지정
b.assign_sub(learning_rate * b_grad)
W.numpy(), b.numpy()
학습
W = tf.Variable(2.9)
b = tf.Variable(0.5)
for i in range(100):
with tf.GradientTape() as tape:
hypothesis = W * x_data + b
cost = tf.reduce_mean(tf.square(hypothesis - y_data))
W_grad, b_grad = tape.gradient(cost, [W, b])
W.assign_sub(learning_rate * W_grad)
b.assign_sub(learning_rate * b_grad)
if i % 10 == 0:
print("{:5}|{:10.4f}|{:10.4f}|{:10.6f}".format(i, W.numpy(), b.numpy(), cost))
plt.plot(x_data, y_data, 'o')
plt.plot(x_data, hypothesis.numpy(), 'r-')
plt.ylim(0, 8)
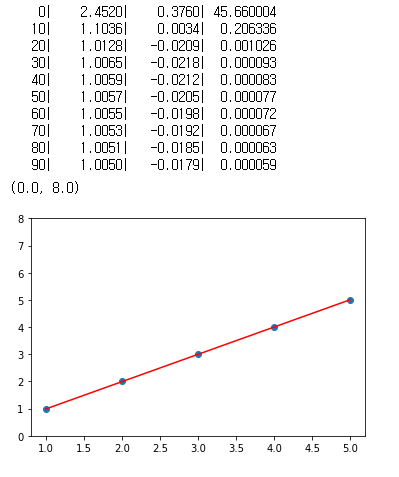
predict
print(W * 5 + b)
print(W * 2.5 + b)